一、梯度下降
梯度下降公式:,,具体细节和代码实现参考文章神经网络介绍
(Batch) Gradient Descent:
### 伪代码
X = data_input
Y = labels
parameters = initialize_parameters(layers_dims)
for i in range(0, num_epochs):
# Forward propagation
a, caches = forward_propagation(X, parameters)
# Compute cost.
cost = compute_cost(a, Y)
# Backward propagation.
grads = backward_propagation(a, caches, parameters)
# Update parameters.
parameters = update_parameters(parameters, grads)
Stochastic Gradient Descent:
### 伪代码
X = data_input
Y = labels
parameters = initialize_parameters(layers_dims)
for i in range(0, num_epochs):
for j in range(0, m):
# Forward propagation
a, caches = forward_propagation(X[:,j], parameters)
# Compute cost
cost = compute_cost(a, Y[:,j])
# Backward propagation
grads = backward_propagation(a, caches, parameters)
# Update parameters.
parameters = update_parameters(parameters, grads)
Mini-Batch Gradient Descent
Mini-Batch Gradient Descent介于(Batch) Gradient Descent和Stochastic Gradient Descent之间,可分为两步进行
- Build mini-batches from the training set (X, Y)
def random_mini_batches(X, Y, mini_batch_size = 64, seed = 0): """ Creates a list of random minibatches from (X, Y) Arguments: X -- input data, of shape (input size, number of examples) Y -- true label vector (1 for blue dot / 0 for red dot), of shape (1, number of examples) mini_batch_size -- size of the mini-batches, integer Returns: mini_batches -- list of synchronous (mini_batch_X, mini_batch_Y) """ np.random.seed(seed) m = X.shape[1] #number of training examples mini_batches = [] # Step 1: Shuffle (X, Y) permutation = list(np.random.permutation(m)) shuffled_X = X[:, permutation] shuffled_Y = Y[:, permutation].reshape((1,m)) # Step 2: Partition (shuffled_X, shuffled_Y). Minus the end case. num_complete_minibatches = math.floor(m/mini_batch_size) # number of mini batches of size mini_batch_size for k in range(0, num_complete_minibatches): mini_batch_X = shuffled_X[:,k*mini_batch_size:(k+1)*mini_batch_size] mini_batch_Y = shuffled_Y[0,k*mini_batch_size:(k+1)*mini_batch_size].reshape((1,mini_batch_size)) mini_batch = (mini_batch_X, mini_batch_Y) mini_batches.append(mini_batch) # Handling the end case (last mini-batch < mini_batch_size) if m % mini_batch_size != 0: mini_batch_X = shuffled_X[:,num_complete_minibatches*mini_batch_size:] mini_batch_Y = shuffled_Y[0,num_complete_minibatches*mini_batch_size:].reshape((1,m % mini_batch_size)) mini_batch = (mini_batch_X, mini_batch_Y) mini_batches.append(mini_batch) return mini_batches - Train the network
### 伪代码 X = data_input Y = labels parameters = initialize_parameters(layers_dims) mini_batches = random_mini_batches(X, Y) for i in range(0, num_epochs): for minibatch in minibatches: # Select a minibatch (minibatch_X, minibatch_Y) = minibatch # Forward propagation a, caches = forward_propagation(minibatch_X, parameters) # Compute cost cost = compute_cost(a, minibatch_Y) # Backward propagation grads = backward_propagation(a, caches, parameters) # Update parameters. parameters = update_parameters(parameters, grads)
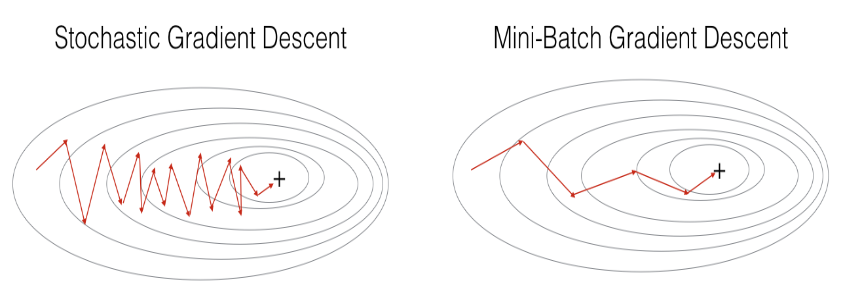
梯度下降、随机梯度下降与mini-batch梯度下降的区别在于进行一次参数更新所使用的训练样本数量;若选取合适的mini_batch_size,mini-batch梯度下降常优于梯度下降和随机梯度下降,特别是当训练数据集很大的情况下。为进一步减少梯度下降过程中不必要的震荡(如下图所示),加快收敛速度,有一些改进的算法可供选择:
Momentum
与
RMSProp
与
Adam
与,其中表示迭代次数
以上算法中的学习率可以是常数,也可以根据训练进度而变化,常用的几种方法有:
learning rate decay
有多种形式,例如,为初始学习率
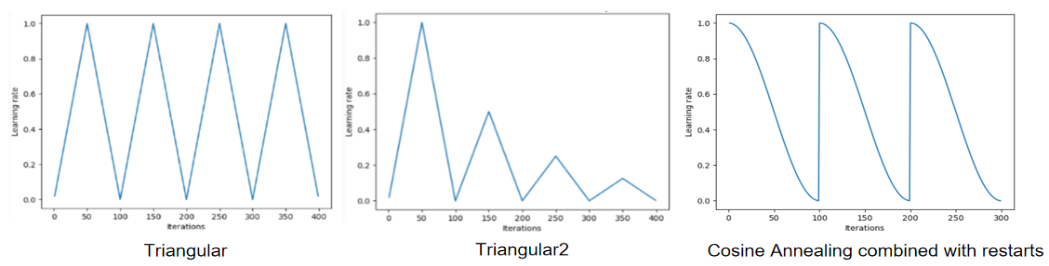
cyclic learning rates
有多种形式,例如下图所示
二、正则化
L2(weight decay)
以二分类问题为例,使用L2正则化后的损失函数为
Dropout
Dropout在每次迭代过程中随机关掉一些神经元,针对矩阵,有矩阵,生成的代码如下所示:
### 伪代码
Dl = np.random.rand(Al.shape[0], Al.shape[1]) # Step 1: initialize matrix D1 = np.random.rand(..., ...)
Dl = (Dl<keep_prob) # Step 2: convert entries of D1 to 0 or 1 (using keep_prob as the threshold)
网络的训练过程和文章神经网络介绍中的基本一致,不同的是:
(1) 在前向传播过程中按文章中的公式计算出后还需要额外进行处理: ,
(2) 在后向传播过程中使用经过处理后的进行计算,并且按文章中的公式计算出后还需要额外进行处理:,
其余训练过程和不加Dropout时的训练过程均相同,但要注意在检验网络或使用网络进行预测时不要使用Dropout(即将keep_prob设为1)
